Resolver un problema de razones usando una gráfica de barras

Las razones son un tema importante en los grados 5-7, y hay muchos problemas verbales que las usan. Por favor lea cuidadosamente lo que sigue - ¡espero que le ayude si tiene dificultades con este tema!

Dave en el blog MathNotations tuvo un problema interesante de razones. Lo he cambiado un poco, para que los números sean más "amigables".

En una escuela bachillerato, la razón entre los alumnos del 11^o grado y los alumnos del 12^o grado es 7:5. La razón entre los chicos del 11^o grado y las chicas del 11^o grado es 4:3. La razón entre los chicos del 12^o grado y las chicas del 12^o grado es 7:3. Que es la razón entre los chicos de 11^o grado y las chicas de 12^o grado?

1. He aquí un diagrama que muestra que la razón entre los alumnos del 11^o grado y los alumnos del 12^o es 7:5.

Como se puede ver en el diagrama, el "total" se divide en 12 partes (7 + 5).

Podríamos usar este diagrama para resolver problemas tales como:

Si hay 768 alumnos en los grados 11 y 12, ¿cuántos alumnos hay en el grado 11? (Divide el total en 12 partes, y luego toma 7 de las partes.)

O...

Si hay 95 alumnos en 12^o grado, ¿cuántos hay en grado 11? (Divide el numero de los alumnos del 12^o grado por 5, luego multiplica el resultado por 7.)

O..

Si hay 49 alumnos en 11^o grado, ¿cuántos alumnos hay en total? (Divide la cantidad de alumnos del 11^o grado por 7, entonces multiplica el resultado por 12.)

Todas estas diviciones y/o multiplicaciones por 5/7/12 se quedan claras al ver el diagrama.

---

PERO, seguiremos en resolver el problema de arriba:

En una escuela bachillerato, la razón entre los alumnos del 11^o grado y los alumnos del 12^o grado es 7:5. La razón entre los chicos del 11^o grado y las chicas del 11^o grado es 4:3. La razón entre los chicos del 12^o grado y las chicas del 12^o grado es 7:3. Que es la razón entre los chicos de 11^o grado y las chicas de 12^o grado?

Usamos este mismo diagrama:

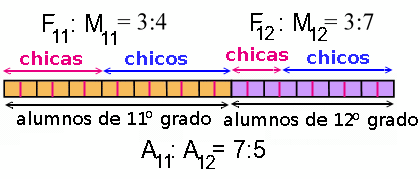
Luego añadimos la información adicional en él.

La razón entre los chicos del 11^o grado y las chicas del 11^o grado es 4:3, lo cual significa que los alumnos del 11^o grado se dividen en 7 partes (4 + 3). En una manera similar, los alumnos del 12^o grado se necesitan dividir en 10 partes.

¡Voila! Lo que pasa (una coincidencia?) es que la division original en 7 y 5 partes sirve muy bien y nos da la division de los alumnos del 11^o grado en 7 partes (ya estan así!) y los alumnos del 12^o grado en 10 partes si solo dividimos cada parte en dos.

Pues, ¿qué es la razón entre los chicos del 11^o grado y las chicas del 12^o grado?

En el diagrama, el TOTAL se divide ahora en 24 partes. Los chicos del 11^o grado representan 8 de las partes, y las chicas del 12^o grado grado son 3 de las partes. Por eso, la razón es 8:3.

---

En mi blog, resolví también el problema original de MathNotations.